
Ana Carvalho, Software Engineer, and Ricardo Saldanha, Head of Innovation @SISCOG | 9 min read
___________
INTRODUCTION
In 1986, SISCOG was founded as an Artificial Intelligence-based company, with the goal of developing decision support software products for application domains that were yet to be defined. At some point SISCOG identified the transportation domain as its niche market and understood that optimizers were a key component of the software products needed in that market. This led to the adoption of SISCOG’s vision and slogan: “Optimizing the Resources of the World”.
Over the years, SISCOG realized that combining Artificial Intelligence (AI) with Operations Research (OR) was the best approach for tackling the hard combinatorial optimization problems that needed to be solved in order to provide useful decision support in the transportation domain.
Operations Research, a branch of applied mathematics, is one of the fields that has contributed with a wide range of methods to the optimizers used daily by transportation companies around the world. Contrary to what most people think, mathematics is more than a set of numbers and abstract formulas. OR techniques can transform complex problems into efficient solutions. Through the application of OR, SISCOG’s products improve companies’ profit, productivity, and, ultimately, passengers’ satisfaction.
This article explains the central role of OR in developing innovative solutions that are then embedded in SISCOG’s products and that impacts millions of people worldwide.
MATH'S ROLE AT SISCOG
Have you ever thought about how OR can be used to …
... generate a timetable?
... plan vehicle operation and maintenance needs?
... produce crew schedules?
When we catch a train each morning to get to work, we are far from thinking about all the mathematics behind it. Let’s take a closer look as we explore the different SISCOG products.
The same train arrives at 7.50 AM at the same station platform every morning. If, for some reason, we miss that train, the next train will arrive at 8.10 AM and then at 8.30 AM. This pattern is repeated at 8.50 AM, 9.10 AM, 9.30 AM, and so on. This is what is called a regular or periodic timetable, and it is created and managed using SISCOG’s ONTIME product.
______________________
ONTIME is responsible for producing and adjusting a timetable, i.e. a set of train trips where each trip is defined by a weekday, a route in the network, start, end and intermediate stopping stations, as well as departure and arrival times at those stations.
Timetables are produced with a two-step process.
- The first step regards the generation of a railroad line plan, which can be defined as a set of unscheduled train trips designed to cover the passenger demand and satisfy as much as possible passenger preferences, but sticking to the limited capacity in terms of track and fleet.
- The second step, called train scheduling, assigns times to the unscheduled train trips making sure that all traffic rules are satisfied and traveling times minimized. The original timetable often needs to be adjusted for specific situations where operating conditions change (e.g. tracks become unavailable, stations are closed, speed limits change, etc.). In this case trains need to be rescheduled, but with a minimum number of changes with respect to the original schedule.
Periodic timetables are a kind of timetables that are usually attractive for passengers since they are regular and easy to memorize. In this kind of timetables trips with the same route or service pattern are equally spaced in time.
The timetable generation problem is a very complex combinatorial optimization problem that is solved by combining AI and OR techniques. For instance, the line planning problem is known to be solved with genetic algorithms, while the train scheduling and rescheduling problems are known to be solved with either (a) SAT combined with mixed-integer linear programming or other OR techniques, (b) SAT combined with reinforcement learning, or (c) MaxSAT. SAT (MaxSAT) is both a way of modeling feasibility (optimization) problems and a set of techniques to solve them. In SAT (MaxSAT) a problem is modeled as a Boolean Satisfiability Problem, which is used to decide whether a propositional formula is satisfiable or not (satisfied in the best possible way).
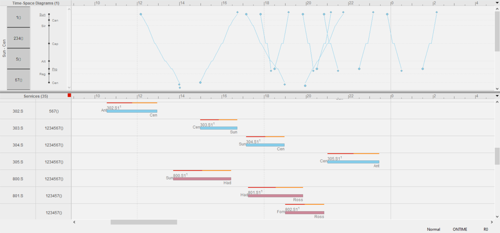
Figure 1 – Example of a timetable solution produced by ONTIME. At the top is a time-space diagram, which is a visual representation of time against the position and movement of trains through the stations between their departure and arrival. At the bottom are the corresponding train trips.
The train we catch every morning has been carefully chosen to meet passengers’ demand through the FLEET product.
______________________
FLEET product is responsible for producing and adjusting vehicle operational plans, which means solving the rolling stock planning problem (RSPP). In short, the RSPP is the problem of assigning vehicles to the timetabled trips scheduled by ONTIME.
In an RSPP, a set of vehicles combined to create a composition (what we typically call “the train”) are assigned to a trip. A composition assigned to a timetable trip considers the expected demand of passengers. Each vehicle in a composition has a set of tasks to do that correspond to sequenced trips, i.e., trips that are operated one after the other (eventually with a time interval between them). Shunting movements can occur to reduce or expand the size of a composition when sequenced with the following trip. Furthermore, vehicles must be maintained frequently, which leads to several additional constraints with different technical needs. RSPP main optimization goal is to minimize the total number of vehicle kilometers (which accounts for energy consumption and maintenance costs) and the fleet size. Additional optimization goals may include maximization of revenue (expected number of tickets sold).
To solve the previously described problem, FLEET considers different approaches involving OR. One of these is mixed-integer linear programming. The possible compositions to be assigned to a trip and the possible shunting movements between sequenced trips can be represented in a graph. Then, considering a flow model, with additional vehicle maintenance constraints, we obtain the optimal solution to the RSPP.

Figure 2 – Example of a solution produced by FLEET. Each row represents the set of tasks for each composition. Each task represents a trip (green) or a maintenance need (yellow).
Our morning routine to get to work finishes after a 30-minute journey. The train arrives at the final station, and we finally reach our destination. The driver left the train; he/she finished his working shift for the day. Can you imagine all the OR behind this work schedule? CREWS product is responsible for that.
______________________
CREWS product is responsible for producing and adjusting crew schedules, taking into consideration the given train timetables and vehicle schedules. Several operational constraints and labor rules are considered, as well as crew skills and preferences. The complexity of this problem is related to the number and duration of tasks to plan and the rules that must be verified. CREWS can also be used to produce and adjust schedules for other types of staff, but crew schedules are far more complex than those of other staff. That’s why we emphasize crew schedules.
In CREWS schedules are produced for a standard week with a two-step process.
- In the first step, called shift scheduling problem, shifts are produced for several operational crew bases resulting in a set of train trip sequences starting and ending in the same operational base complying with labor rules related with working times, meal breaks, transfer times, operational base capacity and many more. The most usual optimization goal is to minimize the number of shifts needed to cover all the work.
- In the second step, called roster scheduling problem, rosters are produced independently for each operational base as sets of shifts sequenced typically in a cyclic manner. These rosters must comply with rules related with days off, working times, operational base capacity and many more. Typical optimization goals are maximizing crew preferences and fairness. The shift and roster rescheduling problems consist in adjusting the original shift and roster schedules to accommodate specific changes in the assumptions under which the original schedules were produced, such as timetable changes, crew absences, etc. Typical goals of rescheduling problems are to cover as much work as possible and to minimize changes with respect to the original schedules.
The shift scheduling and rescheduling problems are usually modeled as a minimum cost set covering problem with additional constraints and are typically solved with several OR techniques, such as Lagrangian relaxation, column generation, dynamic programming and greedy heuristics. The roster scheduling and rescheduling problems are usually solved with OR techniques such as mixed-integer linear programming, constraint aggregation and large neighborhood search. In rescheduling problems local search techniques are also used.

Figure 3 – Example of a solution produced by CREWS for the shift scheduling.
REAL-WORLD CHALLENGES
The problems previously described may not seem difficult to solve if we consider small-scale realities with only a few trips and crew to schedule, and no additional complex constraints. However, this is rarely the case in practice. Real-world problems, namely the ones that are solved by ONTIME, FLEET, and CREWS, include thousands of trips and complex additional constraints. To tackle these real-world challenges, Operations Research has proven highly effective, producing results that have improved both profitability and productivity.
Examples of gains reported by SISCOG clients with the use of optimizers:
- 3%-4% increase in revenue due to better adjustment of seat capacity to demand
- 5%-6% reduction in crew members due to the generation of more cost-efficient schedules
- Up to 90% reduction in crew overtime due to the generation of more cost-efficient schedules
- Up to 60% reduction of human planners due to less manual work
INNOVATION AND COLLABORATIONS
Innovation is a core value at SISCOG and Operations Research plays a key role in sustaining this innovative edge. To maintain this position, SISCOG encourages collaboration with a variety of individuals and organizations. These collaborations take place both internally and externally.
- Internal collaborations are focused on teamwork. Different departments work together, sharing experiences and ideas. Each team member contributes to the overall success of SISCOG.
- External collaborations include partnerships with Universities and Research Centers, with OR being one of the main areas of focus. Each year, SISCOG supervises students working on their Master's or PhD theses and welcomes young talent through internships. In addition, SISCOG participates in events to help students understand the role of OR beyond academia. It is particularly valuable for students to see how their knowledge can be applied to solve real-world problems.
CONCLUSION
SISCOG is continuously focused on innovation, both to provide high-quality, competitive products for existing clients and to attract new ones. Math, and more specifically Operations Research, is recognized as one of the most essential tools to maintain the high innovation standard, namely in ONTIME, FLEET, and CREWS products. In fact, the application of OR techniques has consistently contributed to improving our clients’ profitability, productivity, and quality of transportation service over the years.
Collaborating with diverse stakeholders is also essential to unlocking the full potential of OR and embedding innovation in SISCOG’s products.
Whether you are an engineer, an academic, or a transport operator, we invite you to share your thoughts and ideas about the potential of OR in the public transportation sector.
What new challenges in transportation do you believe Operations Research can successfully answer?
